Don’t hesitate to contact us:
Forum: discuss.graphhopper.com
Email: support@graphhopper.com
There are many terms when it comes to route optimization and route planning. In this blog post we describe the ones we use.
Routing is the process of finding the best path between two or more locations with a fixed order in a road or rail network. The criterion according to which a path is the best can vary. You may be looking for the shortest path (by distance), the fastest (by travel time), but also the most scenic or the safest path. Anything is possible as long as it can be specified by assigning some quantity, a generalized cost, to each road segment, and looking for the least-cost path.
Such paths can be calculated with our Routing API which is powered by our open source routing engine.
Other terms like journey planning, trip planning or route planning are frequently used, sometimes also itinerary planning.
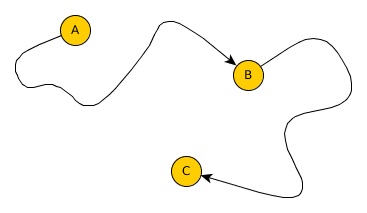
There are a number of algorithms to solve this problem. The most famous ones are Dijkstra’s algorithm, and its accelerated version, the A* algorithm. The following image illustrates how the A* algorithm finds the fastest path between two locations. It explores all roads marked in blue to find the fastest path marked in red:
When we use the term route optimization, we mean solving vehicle routing problems (VRP) and travelling salesman problems (TSP).
These problems can be solved with our Route Optimization API. It can be used to solve various vehicle routing problems like the capacitated VRP with time windows or the VRP with multiple depots. It allows the user to specify a number of business-specific constraints like time windows, multiple capacity dimension, driver skills etc., and it can even be used to solve large scale problems (>1000 locations and >100 vehicles).
The optimization is based on a heuristic approach that cannot guarantee optimal solutions, but, if configured well, it can provide very good solutions fast. The following steps are done under the hood of our Route Optimization API:
The following image shows a typical solution for a capacitated vehicle routing problem with 249 deliveries and 2 depots:
Our Route Optimization API is powered by our open source optimization engine jsprit.
Navigation is
is a field of study that focuses on the process of monitoring and controlling the movement of a craft or vehicle from one place to another
according to Wikipedia. And for us this means that once you found a path in the network, then navigation is the process of guiding you to the destination. It is tightly coupled to an actual device that knows your location and an algorithm that guesses your direction and the road you are on. With the help of our Routing API and Map Matching API, such a process can be implemented. If, for example, you would like to implement an Android app for the driver of a delivery vehicle, you could start with our Java API client.
The distance matrix is a two-dimensional matrix containing distances for all locations to all the other locations. Suppose you have 5 locations A, B, C, D and E, then the distance matrix consists of all 20 distances (5*5-5): A to B, A to C, A to D, A to E, B to A, B to C, and so forth:
Note that the matrix is not necessarily symmetric as you can have one-way roads, and the diagonal is 0 because a location to itself has always the distance of 0. You can calculate this matrix (or, similarly, the travel time matrix) by calling the Routing API multiple times, or much faster, in a single request, with our Matrix API.
Learn more on our website about the GraphHopper Directions API.