Don’t hesitate to contact us:
Forum: discuss.graphhopper.com
Email: support@graphhopper.com
One of the main purposes of our open-source routing engine is calculating the ideal route to get from one place to another. Using publicly available map data from OpenStreetMap it can calculate the optimal route for a given source-target pair for many different vehicles and flexible optimization criteria. However, such route calculations become considerably more involved if not only a single route is required, but let’s say all routes between all of a given set of locations.
This so-called many-to-many routing problem is quite common in different logistic applications, urban planning and especially in route optimization applications. For example to solve the vehicle routing problem (VRP) one first has to obtain a table that includes the traveling costs for all location pairs. This is often called the time/distance table or the cost matrix.
The computational effort to obtain this table quickly becomes significant: For ten locations the table only has a hundred entries, but for, let’s say, 5000 locations it already contains 25 million costs. This means that using a naive approach of calculating the single costs in isolation is not an option as the matrix computation time can quickly approach the order of several days. Even with sophisticated speed-up techniques1 , that allow much faster routing queries than standard algorithms like Dijkstra or A*, it can still take several hours to calculate matrices with thousands of locations. Not exactly what you are looking for if you want to build a highly performant system that requires these matrices. Luckily the matrix calculation leaves a lot of room for performance tweaks and optimizations.
At GraphHopper we know this problem quite well: We receive thousands of route optimization problems every day and an efficient calculation of these matrices is essential. Although this is only one of the many problems we need to solve to provide our services, this already represents a complex challenge in itself. We surely have to make use of state-of-the-art algorithms and optimizations to keep our response times and memory requirements low, but we are not only concerned about performance. More importantly we want to provide highly reliable results that our customers can trust so they can fully focus on the business problem they actually want to solve. Our routing algorithms are guaranteed to find the best routes within the underlying model without making use of any approximation methods. At GraphHopper we are convinced that matching these requirements would be impossible without fully automated testing that covers even the most exotic constellations of the routing network2. This allows us to continuously improve our routing routines knowing that they are still fully functional even after making extensive changes to our algorithms.
Not too long ago we reported about some massive speed improvements of our Matrix API. Today we are happy to announce: We did it again. Just recently, we have overhauled our matrix service to achieve better test coverage and consequently were able to achieve even faster response times than previously.
The following graph shows the calculation time for complete N:N-sized cost matrices including the traveling time, the distance and the cost3 of all N*N routes. For the measurement we used OpenStreetMap data of Europe and created random matrix queries within the city area of Berlin. For comparison we have also included the dashed lines showing the performance we achieved before our latest improvements. Please keep in mind that these results should only show the relative improvements of our algorithms, the absolute times can vary strongly depending on the hardware etc. For example with our current production setup, that uses some better hardware, the response times are even 2 times faster.
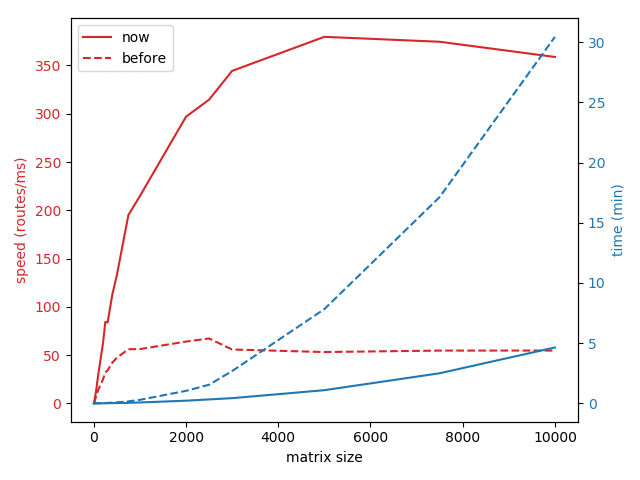
We can see that for 10.000 locations the calculation time takes below five minutes. Not so bad considering that since the matrix contains 100 million costs and it is on single core (no multithreading). That’s more than 350.000 routes per second! Comparing with the blue dashed line we see that with our recent work we have reduced the processing time by more than a factor of six. For 1.000 locations the matrix calculation now takes well below five seconds, much better than approximately 18 seconds it took previously.
While full N:N distance matrices are typical for the route optimization applications we mentioned above, another common need is calculating the costs of traveling to many different destinations from a single source, i.e. calculating 1:N matrices. Here is a similar graph for this so called one-to-many problem:
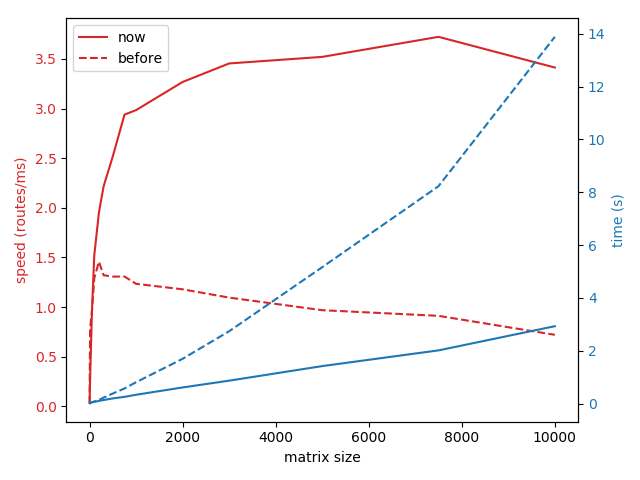
Again we can see quite a significant improvement of the processing time: For example the calculation of a 1×10.000 matrix used to take about 14 seconds, but now can be done in less than three seconds. Note that this time not only includes the time for the matrix calculation on the routing graph, but also the time it takes to resolve and ‘snap’ the coordinates of the matrix request to the closest edges of the graph.
Does this sound interesting ? You can try it yourself, just sign up for a free API key and start using the GraphHopper Matrix API today! You can find detailed documentation of the Matrix API here.
[1] Like Contraction Hierarchies used by GraphHopper.
[2] Note that the OpenStreetMap road network for Europe contains tens of millions of road segments with different road types, narrow bridges, etc. And it is increasing every day.
[3] The ‘cost’ of a route can include a combination of time and distance but also other factors like fuel consumption, road bendiness etc.